LEO, GTO, SSO a další – čím se liší různé orbity?
Na ElonX se můžete setkávat s různými orbitami, na které míří Falcon 9 se svými rozličnými náklady. Dragony míří na ISS na nízké oběžné dráze, zatímco komunikační satelity obvykle letí na tzv. GTO. Orbity se dají dělit podle různých kritérií a náročnost jejich dosažení se liší, což má vliv na volbu rampy a také na možnost přistání. Přichystali jsme pro vás tedy článek, díky kterému si uděláte pořádek v rozličných orbitách.
Orbitální dráha, neboli orbita, je dráha, po které obíhá kosmické těleso kolem těžiště soustavy. Takové těleso může být např. planeta, měsíc, asteroid či kometa při oběhu kolem centrálního tělesa. Orbitální dráhy dělíme na řadu podskupin. Zkusíme si ty nejčastěji používané představit blíže. Rozdělení orbit je možno provést podle centrálního tělesa, výšky oběhu, tvaru dráhy, sklonu vůči rovníku a dalších.
SpaceX až na výjimky vypouští svůj náklad na dráhy, které mají jako své centrální těleso planetu Zemi. Takováto dráha se nazývá geocentrická, s trochou trpkosti je nutno dodat, že s výjimkou antiky tehdejší církev až do 17. století ani jiný typ oběžné dráhy nepřipouštěla. Automobil Elona Muska či družice DSCOVR však byly vyneseny na heliocentrickou dráhu, tělesa na této dráze obíhají kolem Slunce.
Mezi další, již méně používané názvy patří:
- Měsíc – selenocentrická
- Merkur – hermocentrická
- Venuše – afrodiocentrická
- Mars – areocentrická
- Jupiter – joviocentrická
- Saturn – kronocentrická
- Uran – uranocentrická
- Neptun – neptunocentrická
Nyní se přesuneme k naší mateřské planetě, kolem které obíhá náklad společnosti SpaceX nejčastěji, a podíváme se na rozdělení drah podle výšky oběhu.
- Nízká oběžná dráha (LEO z anglického Low Earth Orbit) – tento název se používá pro výšky mezi 150 km a 2000 km. Na této dráze obíhá ISS, kterou společnost SpaceX pravidelně zásobuje, družice Iridium, Paz, Formosat-5, NROL-76 a další. Je zde i Hubblův dalekohled.
- Střední oběžná dráha (MEO – Medium Earth Orbit) – satelity na této dráze obíhají mezi 2000 km a končí ve výšce 35 786 km, tedy ve výšce geosynchronní dráhy. Na střední oběžnou dráhu bude SpaceX vynášet III. generaci družic GPS. Obíhají zde družice GLONASS, Galileo a jiné
- Vysoká oběžná dráha (HEO – High Earth Orbit) – satelit se pohybuje nad geosynchronní drahou. Na tuto dráhu zamířila družice TESS, která je určená k hledaní exoplanet.
Geosynchronní dráha, která tvoří hranici mezi střední a vysokou oběžnou dráhou je velmi důležitá orbita pro nás pozemšťany. Je to taková dráha, kde satelitu trvá oběh Země stejně dlouho jako otočení Země kolem své osy. Geosynchronní dráze se také někdy říká Clarkova dráha. Název odkazuje na známého spisovatele sci-fi Arthura C. Clarka, který jako první v roce 1945 popsal myšlenku, jak zajistit celosvětový příjem signálu pomocí 3 retranslačních družic. Bohužel se mu nepodařilo nápad patentovat, v Británii je totiž potřeba pro udělení patentu dvou fungujících vynálezů. Tudíž v roce 1962 vydal další článek pod názvem Jak jsem přišel o miliardu dolarů vynalézáním Telstaru ve svém volném čase.
Zvláštním případem geosynchronní dráhy je dráha geostacionární, která má nulový sklon k rovníku (GEO). Princip geostacionární dráhy je následující – družice obíhá na orbitě stejnou kruhovou rychlostí v rovině rovníku, jako se Země otáčí kolem své osy. Z pohledu pozorovatele na Zemi pak družice visí na jednom místě na obloze. Velmi hezky celý proces vysvětluje předchozí obrázek. Najděte si spojnici povrchu Země a onoho satelitu na GEO, ukazuje totiž, že kruhová (úhlová) rychlost Země a satelitu je stejná.
Pro přibližnou představu o tom, kolik vlastně telekomunikačních družic a na které pozici se nachází na GEO, přikládám další obrázek (zdrojové PDF). Podotýkám, že obrázek je už staršího data, proto v něm nenajdete družice vynesené SpaceX. Zároveň ale ukazuje velkou akumulaci družic v některých místech a poměrné volno v místě jiném. Celkem je na GEO zhruba 450 družic.
Než definitivně opustíme geostacionární dráhu, bude dobré se ještě podívat na to, jaký prostor je možno pokrýt signálem z geostacionární dráhy jednou družicí. Uvádí se, že družice z každé pozice na GEO může svým signálem pokrývat vždy 41 % povrchu Země.
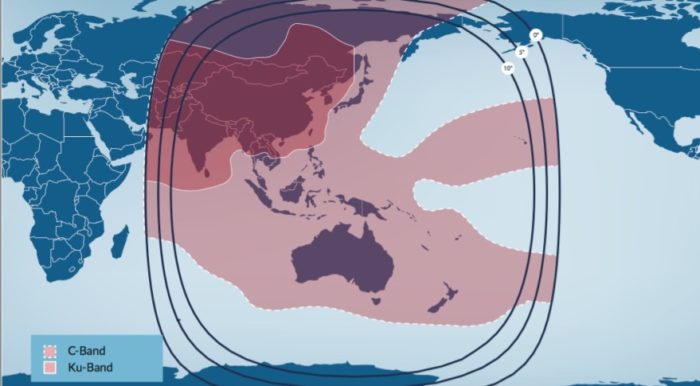
Znázornění oblasti, kterou svým signálem pokryje družice Telstar 18V, kterou SpaceX vynese v létě 2018 (Zdroj: Telesat)
Opusťme už geostacionární dráhu a přesuňme se do dalšího dělení. Dle tvaru je možno dráhy rozdělit na kruhové a eliptické.
Na obrázku výše obíhá planeta okolo centrální hvězdy, už od pohledu se jedná o eliptickou dráhu. Nejvzdálenejší bod od centrálního tělesa se obecně nazývá apoapsida. Nejbližší bod od centrálního tělesa se nazývá periapsida. Na obrázku je centrálním tělesem Slunce, ony body se tedy jmenují perihel (nejbližší) a afel (nejvzdálenější). Pokud je centrálním tělesem Země, nazývá se tento nejbližší bod perigeum, a nejvzdálenější apogeum. S těmito pojmy jste se už určitě setkali, kupříkladu při živých přenosech startů raket, které do češtiny zprostředkovává server Kosmonautix.cz. A pokud je periapsida a apoapsida stejně dlouhá, tj. centrální těleso je ve středu oběžné dráhy, jedná se o dráhu kruhovou.
Nejčastějším cílem společnosti SpaceX je eliptická dráha, konkrétně se jedná o dráhu přechodovou ke geostacionární (Geostationary Transfer Orbit – GTO). Tato orbita je znázorněna na následujícím videu modře, perigeum je ve výšce přibližně 150–200 km (běžná parkovací dráha), a apogeum je ve výšce geostacionární dráhy 35 786 km. Tam, kde končí modrá a začíná červená čára (v apogeu), musí potom satelit zažehnout motor, aby zdvihl perigeum své dráhy rovněž do výšky geostacionární dráhy. V praxi se toto samozřejmě neděje jediným dlouhým zážehem, ale probíhá to postupně. Na tomto odkazu je to podrobně rozkresleno a ukázáno.
Existuje i velice hezká stránka stuffin.space, která vám znázorní dráhu satelitu, který si vyberete, centrálním tělesem je Země. Ovládání je poměrně intiutivní, a rychle ho pochopíte. Zkuste si kupříkladu dát vyhledat některý nedávno vypuštěný satelit určený pro GEO, dráha GTO vám bude ihned jasná.
Posledním rozdělením, které v tomto přehledu orbitálních drah zmíním, je rozdělení podle sklonu orbitální dráhy, neboli podle inklinace.
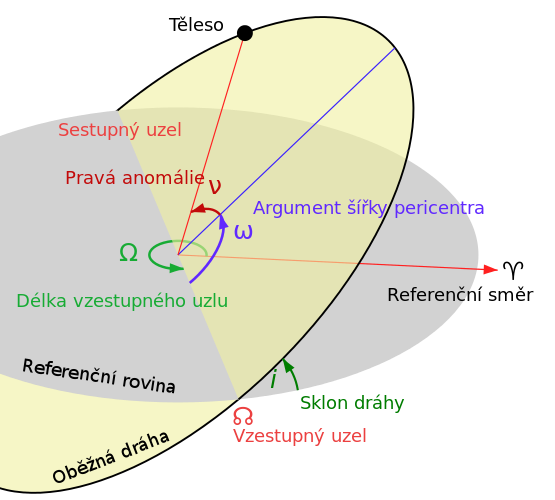
Elementy orbitální dráhy (Zdroj: Wikipedia)
Pro tělesa obíhající okolo Slunce je referenční rovinou ekliptika, pro tělesa, nebo družice, obíhající okolo Země, je to rovina rovníku.
- Pokud je sklon dráhy roven 0°, znamená to, že satelit obíhá v rovině rovníku tzv. prográdně, tedy ve směru otáčení planety Země. Většina satelitů, které obíhají Zemi se sklonem 0° k rovníku, se nachází na geostacionární dráze.
- Pokud je sklon mezi 0–90° obíhá satelit ve směru otáčení planety Země. Vhodným příkladem pro takovouto dráhu je například ISS se svým sklonem 51,6° k rovníku.
- Při sklonu 90° se jedná o polární orbit, kdy družice při svém pohybu přelétává přes póly. Zde jsou velice známým příkladem družice Iridium, meteorologické satelity, či mapovací družice.
- Při sklonu dráhy větším než 90° se jedná o retrográdní oběh, tedy proti směru otáčení Země.
V praxi se označení polární dráha používá nejen pro sklon 90°, ale i pro hodnoty blízké. Proto je tedy v předchozím odstavci zmíněno, že na polární orbitě jsou i družice Iridium NEXT, které mají ve skutečnosti sklon 86,4° k rovníku. A jak vlastně vypadá činnost takové mapovací družice na polární oběžné dráze, ukazuje následující video.
Velmi blízko k polárním oběžným drahám má i heliosynchronní dráha. Jedná se o velmi zajímavou oběžnou dráhu. Je to geocentrická dráha kombinující sklon a výšku oběhu tak, že satelit přelétá nad určeným povrchem Země vždy ve stejný sluneční čas, toto je velmi vhodné pro mapující a špionážní satelity. Satelity na této dráze pracují často ve výškách cca 600–800km a mají 98° sklon vůči rovníku. Z nákladů společnosti SpaceX na této dráze pracují například Paz a Formosat-5. Z budoucích misí tam zamíří SAOCOM-1A či SSO-A.
Následující video znázorňuje princip heliosynchronní dráhy. Na videu satelit obíhající Zemi prolétá neustále na hranici světla a stínu, jeho solární panely budou tedy neustále osvětlovány Sluncem. Zároveň bude zobrazovat povrch Země někdy k ránu, kdy budovy, stromy a další objekty budou vrhat stíny. A proč by měly předměty vrhat stíny? Třebas už jen proto, abyste z oběžné dráhy dokázali poznat, zda objekt, který vidíte, ční do výšky, či zda se zavrtává do země. Nebo kupříkladu proto, že jste schopni z délky stínů známých objektů odhadnout výšku objektů neznámých.
Na samotný závěr přikládám malou tabulku, která ukazuje, jak je vybírán kosmodrom pro start raket Falcon 9 s ohledem na cílovou dráhu. SpaceX potřebuje rampy na obou pobřežích USA, aby dokázalo létat na všechny běžně žádané orbity.
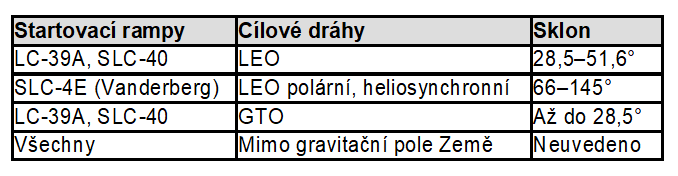
Aby SpaceX mohlo létat na polární orbity, potřebuje rampu na Vandenbergově letecké základně, odkud jsou tyto starty možné. Z floridského Mysu Canaveral se momentálně na polární orbity startovat nedá, ale to se možná časem změní. Nedávno se objevila zpráva, že letectvo zvažuje povolení startů na polární orbity i z Canaveralu. Podmínkou však bude, aby raketa disponovala autonomním destrukčním systémem. Tuto podmínku zatím splňují jen rakety Falcon 9 a Falcon Heavy. Více informací o tomto novém polárním koridoru najdete ve starších Rychlozprávách.
Co se týče plánované rampy v jižním Texasu poblíž Brownsville, tam bude SpaceX z hlediska potenciálních střeleckých koridorů značně omezeno. Spojené státy totiž z bezpečnostních důvodů nepovolují přelety přes obydlené oblasti a u startů z Brownsville ve většině směrů překáží buď Florida, Mexiko, nebo Kuba. Tato studie odhaduje, že jednou z mála možností bude startovat východně nad mezerou mezi Kubou a Floridou. Tento směr je vhodný pro mise mířící na GTO nebo mimo Zemi. Možná právě proto bude tato nová rampa nejspíš už od začátku uzpůsobená primárně pro marsovské BFR. Falcony mohou nadále létat ze tří současných ramp.
Jak vidíte, problematika oběžných drah je docela věda, ale díky tomuto článku v ní snad máte trochu větší jasno. V budoucnu na něj volně navážeme a vysvětlíme si, jak mají různé orbity vliv na nosnost rakety Atlas V a také jak omezují možnosti přistání prvního stupně Falconu 9.
Děkuji Pavlu Vantuchovi za velmi podnětné komentáře a pomoc při psaní článku.
- Mise Fram2 - 24. 3. 2025
- Novinky o soukromé misi Fram2, při které vesmírní turisté jako první lidé přeletí nad zemskými póly - 23. 3. 2025
- Mise NROL-69 - 19. 3. 2025







(Včera jeden, dnes taky jeden muj komentář čeká na schválení …)
Asi bych jen doplnil to, že různé orbity se liší tím, co je po nich uživatelsky požadováno. Jedná se např. o pokrytí území signálem družice, latenci signálu, výhled (nejmenší elevaci nad obzorem) nutnou pro fungování pozemní stanice.
Dále: i když mám zaměřenou parabolu na satelit na GEO, tak musím počítat s tím, že cca 10° kolem paprsku nesmí nic být, abych mohl dobře fungovat.
A taková perlička: družice na GEO má být v kvádru 35km x 35km x 75km, aby byla dobře. Jinak je třeba ji dorovnávat.
Nu, klidne to sepis podrobneji, zni to zajimave a za sebe rad rikam, ze si to moc rad prectu, pokud to nebude moc slozite. 😉
Co mám v poznámkách ohledně orbit a satelitů …
Na satelity okolo Země působí gravitačně všechny okolní hmotná tělesa, především Země, Slunce, Měsíc, Mars a Jupiter.
Když chce satelit změnit výšku, tak pro její snížení musí zrychlit. Když zpomalí, vzdálí se od Země. (tj. v=√(G.M / r) [m/s].
LEO – je sice od 160km, ale teprve od výšky 300km není tak výrazný odpor (vliv) pozemské atmosféry, proto jsou satelity uimísťovány zpravidla výše, nad 300 km od Země. Kromě Apolla byly všechny lidské pilotované lety na LEO. Při větší aktivitě Slunce atmosféra více brzdí, ve špičce Sluneční aktivity musí provádět satelity korekce dráhy každé 2-3 týdny pro udržení výšky.
GEO – Jelikož gravitační pole okolo Země není homogenní vlivem okolních hmotných těles, je nutno družice stabilizovat, tedy brzdit či urychlovat ve svém pohybu na orbitě, jsou zde umisťovány komunikační a meteorologické družice, jedná se o dráhu viditelnou mimo polární oblasti od 81. rovnoběžky k pólu).
Umístění satelitů záleží i na existenci Van Allenových pásů (maxima cca ve 3.000km a 15.000km vzdálenosti od Země), těm (tedy vysokoenergetickým protonům a záření beta) se snažíme vyhýbat, pokud to jde. Např. Hubbleův teleskop se při průletu Van Allenovými pásy vypíná.
Na LEO, MEO a GEO funguje záchranářská konstelace Cospas-Sarsat, sdružení 44 zemé a organizací.
Do rozhodnutí jak zvolit komunikační model satelitu mluví i to, jak můžu a chci mít řešitelnou (velkou, přenositelnou, žravou) klientskou stanici. S dvojnásobkem vzdálenosti k satelitu motřebuji 4x větší energii na vysílání.
Jelikož jsou satelity globální a ne něčí, tak spadají do globální regulace, do kompetence ITU (viz např. https://www.itu.int/ITU-R/go/space/snl/en).
Nějaký přehled satelitů je i na https://www.satbeams.com/satellites, včetně pokrytí nebo elevace a azimutu pro zaměření signálu satelitu.
Prostě, jak tam nasypeš moc odkazu, tak nastává problém, že to systém vyhodnocuje jako spam. A musí to schválit admin. Dle mých zkušeností je to 2 odkazy a více. Lépe by to asi řekl Petr Melechin.
Hezké doplnění, já bych zase napsal, že proto se LEO cca 150-200 km používá jako parkovací, rozšiřuje to startovní okno a máš jistotu, že ona dráha je prostě prosta čehokoliv.
Ten tvůj seznam satelitů na GEO je hezčí, než ten můj, přiznávám. A k tomu udržení paliva na GEO, pokud se nepletu, tak to Dan Heřt na forech kosmonautixu uváděl cca delta v řádu jednotek metrů/s za rok. Tam mě docela taky zaráží, že tam nechají některé satelity taky se klimbat (inklinovat), protože jim pomalu dochází palivo. I to možná souvisí s tím, jak píšeš, že kolem pozice potom musí být na obloze čisto.
To že od 81° je satelit na GEO neviditelný sem nevěděl, respektivě věděl jsem, že pokrytí není až po pól, ale hodnotu jsem přesně neznal.
A zajímavá informace ohledně toho Hubbla.
Díky.
Je to tak, 2 a více odkazů a putuje to do spamu, načež to musím manuálně schválit. Každopádně jsem ten limit zvýšil na 4 a více odkazů, tak snad se už nebude moc často stávat, že komentář neprávem skončí ve spamu. 🙂
“Když chce satelit změnit výšku, tak pro její snížení musí zrychlit. Když zpomalí, vzdálí se od Země.”
Nechtěl bych se hádat, ale tomuhle tvrzení se mi nechce věřit. Čistě laicky jsem si to vždycky představoval takhle:
Když bude zážeh trvat celý jeden oběh, urychlení povede ke zvýšení orbity a naopak. Jakýkoli kratší zážeh by udělal z kruhové dráhy elipsu. Urychlením myslím zážeh ve směru oběhu. Pokud by se udělal zážeh “vzhůru”, tedy směrem od těžiště soustavy (centrálního tělesa), tak bychom dosáhli zpomalení oběhu. A naopak.
Nebo se mýlím?
Tady by byl na odpověd daleko lepší Dušan Majer, to říkám narovinu. A proto přikládám na toto téma jeho vlastní článek.
Pokud vím, pro změnu rychlosti se dělají se zážehy po směru letu a proti směru letu. Tj. loď se buď urychluje, nebo zpomaluje. Neřešme teď změnu sklonu, o to nám tu zjevně nejde. Při urychlování se zvedá apoapsida, při zpomalování klesá apoapsida. Např. pokud se chce přistávat, sníží se apoapsida do atmosféry. Zážehy se nedělají samozřejmě během celého oběhu, nejúčinější by byl v apoapsidě, a to takový, který by byl superkrátký ale zato vydatný, což zase nejde, proto se to dělá na několikrát. Viz. Dušanův přenos startu družice Exomars 2016 na raketě Proton.
Já už asi možná vím, kde nastal nesoulad mezi Vencourem a Tomášem Vodičkou. Každý má svým způsobem pravdu, ale podle mě to Vencour nevyjádřil nejšťastněji. Chtěl podle mě napsat toto. Pokud jsme na stejné dráze (výška, sklon atd) jako objekt, který chceme dohonit, tak nejrozumější způsob, jak cíl dohonit, je udělat něco naprosto nelogického, provedeme zážeh proti směru letu (retrográdní, jak říká Dušan), tím snížíme apoapsidu, dostaneme se na nižší orbitu, kde doženeme cíl (tato orbita má kratší periodu oběhu), jednoduše řečeno, jsme na ni rychlejší než cíl a pak provedeme finální prográdní zážeh, kde cíl opět dorovnáme výšku cíle a jsme u něj. Američané tyto problémy zjistili už v roce 1965 u Gemini 4. A podobným způsobem stíhali Solovjov a Kizim v roce 1986 nejdříve z Miru Saljut 7 a posléze obrácene ze Saljutu 7 Mir.
Děkuji za podrobnou odpověď. Teď už mi to dává smysl.
Na to jak zrychlit, nebo zpomalit a v jakém směru je fajn například Kerbal space program (KSP). Ten mne tyto věci naučil.
Jednoduše, pokud mám kruhovou orbitu a v jednu chvíli zrychlím, pak protilehlý bod na orbitě (za tělesem, kolem kterého se obíhá, tedy po 180°) se vzdálí od obíhaného tělesa. Tedy ano, z kruhu vytvořím elipsu. V KSP, pokud chci z jedné dokonale kruhové orbity udělat orbitu dokonale kruhovou orbitu o větším poloměru, stačí udělat dva zážehy. V jednom místě (v tu chvíli se na druhé straně vytvoří apogeum, které se zvyšuje (vzdaluje od povrchu planety). Poté obletím planetu na druhou stranu (o 180°) a druhý žážeh udělám právě v tomto vzniklém apogeu. V tu chvíli se perigeum (v místě prvního zážehu) začne také vzdalovat až dosáhne stejné výšky, jako apogeum, a opět máme kruhovou dráhu.
Pokud provedu zážeh ne ve směru prograde (v tečném směru k orbitě, kdy se urychlím), ale v normále (ve směru osy vedoucí ze středu obíhaného tělesa a satelitu), pak se opět z kruhové dráhy tvoří elipsa, ale tentokrát upravuju apogeum a perigeum na ose kolmé, proti předchozí situaci. Tedy teoreticky se mění body za čtvrt orbity a za tři čtvrtě orbity od místa, kde zážeh provádím. Výška v místě, kde zážeh provádím a na druhé straně by se měnit neměla. Tak říkajíc natáčím orbitu kolem místa, kde provádím zážeh do elipsy, kdy jeden střed je stále ve středu obíhaného tělesa a druhý nově vytvořený je na ose kolmé
Jak se bude měnit orbita se dá nakreslit i graficky. Pokud si nakreslím kružnici, a v jednom bodě si nakreslím úsečku tečnou ke kružnici, kde délka úsečky bude znázorňovat orbitální rychlost a pak nakreslím úsečku ve směru kam urychluji o délce odpovídající změny rychlosti, a graficky tyto dva vektory sečtu dostanu výsledkou orbitální rychlost. A to velikost (délka úsečky), i směr těčný na elipsu. Pokud tedy urychluji prográdně (jednoduše zrychlím jako v prvním případě), pak obyčejně sečtu obě délky úsečky, a směr nové rychlosti bude v původním směru, protože při zrychlení se obe překrývají a jsou shodně orientované). Pokud se brzdí, pak nakreslím původní vektor v původním směru a opačný vektor v opačném směru. Pokud se urychluje po normále, nakreslím vlastně kolmou úsečku na původní vektor rychlosti. A pokud obě úsečky graficky sečtu, dostanu obdélník. A nový vektor rychlosti bude úhlopříčka tohoto obdélníku s počátkem v místě zrychlení.
Strašně těžko se slovně vysvětluje to, co se kreslí na papír, když to tady nemohu nakreslit. Popisuju to možná až moc jako pro de***y, a pravděpodobně to z toho ani není pochopitelné, ale právě proto, že to popsat jen slovy bez kreslení není jednoduché, snažím se to popisovat co nejpodrobněji. Zkusím najít nějaké odkazy, kde jsou tato grafická řešení nakreslená. Ale to až později.
Mám to odsud, z Coursery … Introduction to Satellite Communications, Orbits, Overview (https://www.coursera.org/learn/satellite-communications/lecture/J248k/overview), zhruba v čase 4:20, doporučuju zapnout anglické titulky.
Pěkné, dík.
Nějaký přehled satelitů je i na https://www.satbeams.com/satellites.
Bude zmíněn i vliv slunečního větru? Tj. změna pozice na GEO během 24 hodin?
Veľmi pekný článok. Vďaka za veľa nových informácií. 🙂 Možno by sa hodil ešte článok o štartovaciom okne, kedy môže byť vypustená raketa, viem že to záleží od cieľovej dráhy, ale zaujímalo by ma či sa do tohto okná berie na vedomie poloha ostatných družíc aby nedošlo k stretu počas štartu. Ďakujem za odpoveď. 🙂
Díky za pochvalu, jsem rád, že se líbil.
Jak to tak čtu, ten dotaz, bude dobré to zabudovat do druhého dílu, protože je to dost dobrá poznámka a připomínka. Půl hodiny sem hledal odpověd na internetu, než sem nějakou našel a přitom byla pod nosem a já si jí nevšiml. Logika sice říkala, že startovní okno by to mělo brát v potaz, ale protože nerad tvrdím něco, co nemám podloženo, nebo o čem si nejsem 100% jistý, tak jsem pořád hledal a našel. Po vypočtení okna dochází potom ještě ke kontrole na tzv. COLA (Collision On Launch Assessment), prostě se zjistí, jestli při letu nehrozí kolize s čímkoliv nahoře, nebo i jen velké přiblížení. Dál jsem v tom zatím nepátral, tohle mi pro odpověd zatím stačilo :-).
diky za článok a som o niečo mudrejši 😀
Dobrý den, díky za pěkný článek. Měl bych ovšem poznámku k heliosynchronní dráze – podle klasické nebeské mechaniky přece není možné aby jakákoli družice setrvale obíhala nad hranicí světla a stínu bez neustálých průběžných korekcí roviny oběhu. Mějme rovinu T, na níž leží hranice světla a stínu na povrchu planety obíhající kolem slunce. Tato rovina je vždy kolmá ke spojnici planety a Slunce, bez ohledu na rychlost a orientaci osy rotace planety. Je-li dráha planety kolem slunce přesně kruhová, potom rovina T rotuje kolem osy kolmé k rovině oběhu planety úhlovou rychlostí přesně rovnou úhlové rychlosti oběhu planety kolem slunce. V případě Země je to 1 otočka za rok. Pokud tedy pracujeme s klasickou newtonovskou nebeskou mechanikou, je takováto oběžná dráha nemožná, jelikož orientace rovin oběžných drah v prostoru se nemění. Znamená to snad, že tento typ dráhy nějak počítá s relativistickými změnami oběžné roviny? Nebo je družice na této dráze pouze po přechodnou dobu (několik dní v roce)?
Dobrý den i vám, děkuju moc, jsem rád, že se líbil.
Při psaní téhle části, o SSO dráze, jsem vycházel z přehledových článků na wiki, či kupříkladu zde. Pro typické dráhy a sklony jsem se zase nechal inspirovat příručkou SpaceX z roku 2009 a výkony rakety Falcon 9 1.0 block 2, či tou krátkou tabulkou na wiki, která pojednává o tomtéž. Pasáž měla o SSO měla být spíš představením zajímavé, málo znamé, ikdyž hojně používané dráhy, než nějakým podrobnějším rozborem, na který si upřímně vůbec netroufám. Dopředu říkám, nejsem na dotaz schopen dostatečně fundovaně odpovědět, jsem povoláním makromolekulární chemik, nikoliv fyzik. Přesto se o to alespoň částečně pokusím, kupříkladu, při hledání informací sem narazil na družici RadarSat/SAR, která přesně obíhá na Dusk/Dawn dráze, kterou zmiňujete. Přijde mi, že pokud tato družice primárně spoléhá na solární články a nikoliv na baterie, neměla by tato údálost nastávat několikrát do roka, ale spíše daleko častěji, ale mohu se mýlit. Pokud jde o relativistické změny oběžné roviny, netuším, a hádat zde si vůbec netroufám.
Já se v tomhle taky nevyznám, ale třeba bude vědět někdo z ostatních čtenářů. 😉
Děkuji za odpověď. 🙂 Už jsem se dogoogloval k vysvětlení. Tento typ dráhy využívá orbitální precesi, tedy stáčení roviny oběžné dráhy, které je možné díky ne dokonale sférickému tvrau Země (zemský elipsoid, geoid). Oběžná dráha také musí mít přesně danné parametry k tomu, aby precese byla ve shodě s oběhem Země kolem Slunce. V případě planety s dokonaleji kulovitým tvarem (např. Venuše) by to opravdu nefungovalo, dráha by se musela aktivně korigovat. Pokud jsem to správně pochopil, ani relativistická fyzika k vysvětlení není třeba, stačí pouze “komplexnější” newtonovský popis zahrnující prostorové rozložení hmoty centrálního tělesa. Viz. https://en.wikipedia.org/wiki/Sun-synchronous_orbit
Taky nejsem fyzik (pro změnu programátor) a mé znalosti fyziky zatím končí někde u 1. ročníku VŠ. Každopádně myslím, že by se hodilo do článku přidat aspoň malou poznámku ohledně tohoto jevu, protože to nabourává klasickou “středoškolskou” představu o nebeské mechanice a u řady čtenářů by to mohlo vést ke zmatečným představám nebo podobnému logickému rozporu, jako se to stalo mně. 🙂
Krása. Ďakujeme. PS: odporúčam aj appku NASA Eyes, kde sa môžete pokochať množstvom satelitov na rôznych zaujímavých orbitách aké má napr. satelit TESS, porovnať si ich veľkosť s osobou či školským autobusom a iné zaujímavé veci 🙂